Soil

Water can infiltrate into the soil if the surface is permeable. Spatially distributed infiltration is either based on a soil map or on land use with pre-defined infiltration parameter for each zone. These parameters are then fed into the infiltration model. Additionally, impermeable surfaces, e.g. paved areas, are considered and can be specified from land use, raster or shape files. In these areas no infiltration occurs. For nature-based solutions, such as green roofs, a two-layer Green–Ampt model is used with the possibility of including a constant loss rate and a storage depth.

Infiltration Model

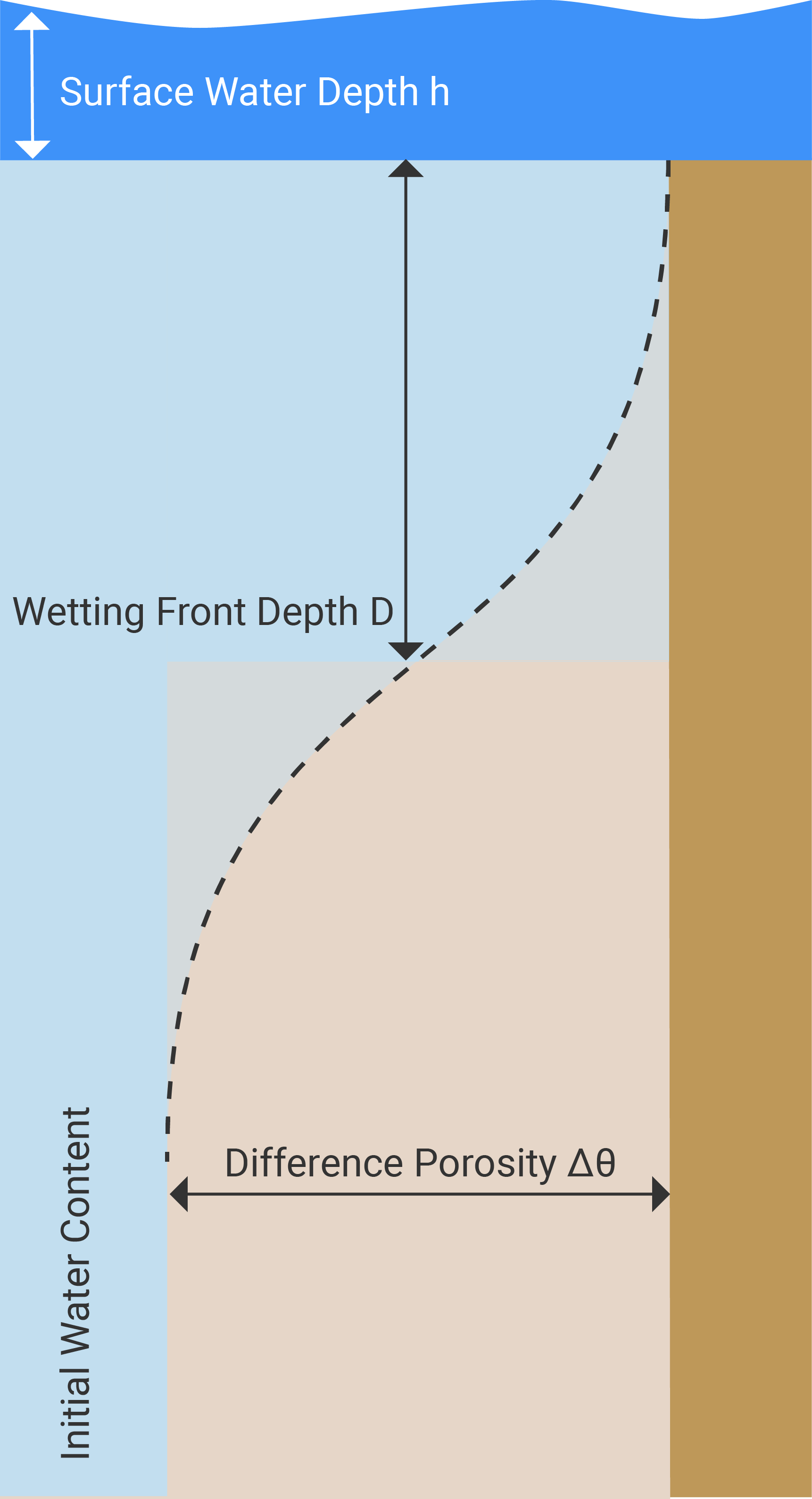
Infiltration curves are either calculated using the Green–Ampt model or a saturated model. The latter assumes saturated soil conditions with a constant infiltration rate \( f \) equal to the saturated hydraulic conductivity \( K_s \).
The Green–Ampt model is a semi-physical model accounting for the ponding surface water height \( h \) and considering three infiltration parameters:

the saturated hydraulic conductivity \( K_s \),
the suction head along the wetting front \( \psi \),
the moisture deficit or effective porosity \( \Delta \theta \).

The saturated hydraulic conductivity \( K_s \) represents an asymptotic limit of the infiltration rate \( f \) as time approaches infinity. In other words, the infiltration rate is always greater than the saturated hydraulic conductivity, but this difference diminishes as time approaches infinity.

In the Green-Ampt model, the cumulative infiltration \( F \) up to time \( t \) is given by:

\[ \int_0^{F(t)} \frac{F}{F + (\psi + h) \, \Delta\theta } \, dF = \int_0^t K_s \, dt . \]

Solving for the infiltration rate \( f \) one obtains:

\[ f(t) = \frac{dF}{dt} = K_s \left[ \frac{ ( \psi + h ) \, \Delta\theta}{F(t)} + 1 \right]. \]

In each cell, surface water permeates into the soil based on the current infiltration rate until the wetting front depths exceeds the soil thickness.

The infiltration parameters are defined based on the infiltration zones. These parameters are typically derived from literature values, such as those provided by Rawls et al. (1983) or Smith et al. (2002).

Temporal Discretization of the Runoff Model

The Green-Ampt model is discretized in time with the implicit Euler method. The infiltration depths \( F \) at time step \( t_{n+1} \) is given by :

\[ F^{n+1} = \frac{1}{2} \big( F^n + K_s \Delta t \big) + \frac{1}{2}\sqrt{ \left( F^n + K_s \Delta t \right)^2 + 4 \, K_s \Delta t \, \Delta \theta \left( h_0^n + \Psi \right)} \]

Even though the infiltration rate is undefined for \( F = 0 \) the implicit Euler method yields a well-defined infiltration depth close to zero, in contrast to the explicit Euler method. If the infiltration depth increment \( \Delta F^n = F_{n+1} - F_n \) exceeds the available surface water depth, it is restricted to ensure a nonnegative surface water depth. The effective infiltration rate \( f_e^n \) is:

\[ f_e^n = \frac{1}{\Delta t^n} \min(\Delta F^n, h^n) \]

where \( \Delta t^n \) is the CFL-limited timestep of the overland flow for timestep \( n \). The precipitation rate \( p_e \) and infiltration rate \( f \) is combined into a single effective runoff increment \( \Delta r_e^n \):

\[ \Delta r_e^n = \Delta t^n \left( p_e^n - f^n \right), \]

which is then applied in the runoff source or sink term \( \mathbf{S}_r \) in the surface water model.

References

Rawls, W.J., Brakensiek, D.L., and Miller, N., 1983. Green--Ampt infiltration parameters from soils data. J. Hydraul. Eng. 109 (1), 62–70.
DOI: 10.1061/(asce)0733-9429(1983)109:1(62)

Chow, V.T., Maidment, D.R., and Mays L.W., 1988. Applied Hydrology. McGraw Hill, 277.

Smith, E., Smettem, R.J., Broadbridge, P., Woolhiser, D.A., 2002. Infiltration theory for hydrologic applications. American Geophysical Union.
DOI: 10.1029/wm015

Buttinger-Kreuzhuber, A., Konev, A., Horváth, Z., Cornel, D., Schwerdorf, I., Blöschl, G., and Waser, J., 2022. An integrated GPU-accelerated modeling framework for high-resolution simulations of rural and urban flash floods. Environ. Modell. Softw. 105480.
Publication available online: 10.1016/j.envsoft.2022.105480